【Note】 线性回归分析(二)——多元线性回归
条评论There are AMP pages for mobile phone.
LRA系列的第二篇,介绍多变量线性回归模型
手敲\(\LaTeX\)难免出现纰漏,有任何疑似错误或者不清楚的地方请直接在下方评论区留言,谢谢各位读者。
模型假设
对于 \(Y_i=\beta_0+\beta_1 X_{i,1}+\beta_2 X_{i,2}+\ldots+\beta_{p-1} X_{i,p-1}+\varepsilon_i\),其矩阵形式为
\[ \begin{pmatrix} Y_1 \\ \vdots \\ Y_n \\ \end{pmatrix}= \begin{pmatrix} 1&X_1&\dots&X_{1,p-1} \\ \vdots&\vdots&\ddots&\vdots \\ 1&X_{n,1}&\dots&X_{n,p-1} \\ \end{pmatrix} \begin{pmatrix} \beta_0\\ \vdots \\ \beta_1 \\ \end{pmatrix} + \begin{pmatrix} \varepsilon_1 \\ \vdots \\ \varepsilon_n \\ \end{pmatrix} \]
接下来的内容和一元回归模型中的最后一节几乎完全一样,这里只做简单抄录。
\[\mathbb{E}\{\boldsymbol{Y}\}=\boldsymbol{X}\boldsymbol{\beta}\] \[\mathbb{E}\{\varepsilon\}=\boldsymbol{0}\] \[\sigma^2\{\boldsymbol{Y}\}=\sigma^2\{\boldsymbol{\varepsilon}\}=\sigma^2\boldsymbol{I}\] \[Q=(\boldsymbol{Y}-\boldsymbol{X}\boldsymbol{\beta})^\intercal(\boldsymbol{Y}-\boldsymbol{X}\boldsymbol{\beta})\] \[\boldsymbol{b}=(\boldsymbol{X}^\intercal\boldsymbol{X})^{-1}\boldsymbol{X}^\intercal\boldsymbol{Y}\] \[\mathbb{E}\{\boldsymbol{b}\}=(\boldsymbol{X}^\intercal\boldsymbol{X})^{-1}\boldsymbol{X}^\intercal\boldsymbol{X}\boldsymbol{\beta}=\boldsymbol{\beta}\] \[\sigma^2\{\boldsymbol{b}\}=\sigma^2(\boldsymbol{X}^\intercal\boldsymbol{X})^{-1}\] \[\boldsymbol{\widehat{\boldsymbol{Y}}}=\boldsymbol{X}(\boldsymbol{X}^\intercal\boldsymbol{X})^{-1}\boldsymbol{X}^\intercal\boldsymbol{Y}\overset{\Delta}{=}\boldsymbol{H}\boldsymbol{Y}\] \[\mathbb{E}\{\widehat{\boldsymbol{Y}}\}=\boldsymbol{H}\boldsymbol{X}\boldsymbol{\beta}=\boldsymbol{X}\boldsymbol{\beta}\] \[\sigma^2\{\widehat{\boldsymbol{Y}}\}=\boldsymbol{H}(\sigma^2\boldsymbol{I})\boldsymbol{H}=\sigma^2\boldsymbol{H}^2=\sigma^2\boldsymbol{H}\] \[\boldsymbol{e}=\boldsymbol{Y}-\boldsymbol{\widehat{Y}}=(\boldsymbol{I}-\boldsymbol{H})\boldsymbol{Y}\] \[\mathbb{E}\{\boldsymbol{e}\}=(\boldsymbol{I}-\boldsymbol{H})\boldsymbol{X}\boldsymbol{\beta}=\boldsymbol{0}\] \[\sigma^2\{\boldsymbol{e}\}=\sigma^2(\boldsymbol{I}-\boldsymbol{H})\] \[\mathrm{SSE}=\boldsymbol{e}^\intercal\boldsymbol{e}=\boldsymbol{Y}^\intercal(\boldsymbol{I}-\boldsymbol{H})\boldsymbol{Y}\] \[\boldsymbol{X}_h=(1,X_h)^\intercal\] \[\boldsymbol{\widehat{Y}}_h=\boldsymbol{X}_h^\intercal\boldsymbol{b}\] \[\mathbb{E}\{\boldsymbol{\widehat{Y}}_h\}=\boldsymbol{X}_h^\intercal\boldsymbol{\beta}\] \[\sigma^2\{\widehat{\boldsymbol{Y}}_h\}=\sigma^2\boldsymbol{X}_h^\intercal(\boldsymbol{X}^\intercal\boldsymbol{X})\boldsymbol{X}_h\]
方差分析
分析过程同样和一元的方差分析并无二致
\[\sum_{i=1}^{n}(Y_i-\widehat{Y})^2=\sum_{i=1}^{n}(Y_i-\widehat{Y}_i)^2+\sum_{i=1}^{n}(\widehat{Y_i}-\bar{Y})^2\] \[\mathrm{SSTO}:(n-1)=\mathrm{SSE}:(n-p) + \mathrm{SSR}:(p-1)\]
| Source | SS | df | MS | F |
|---|---|---|---|---|
| Model | SSR | \(p-1\) | SSR/\((p-1)\) | MSR/MSE |
| Error | SSE | \(n-p\) | SSE/\((n-p)\) | |
| Total | SSTO | \(n-1\) |
\(F\)检验
关于\(H_0:\beta_1=\ldots=\beta_{p-1}=0\)的\(F\)检验为
\[F^\ast=\frac{\mathrm{MSR}}{\mathrm{MSE}}\sim F_{p-1,n-p}\]
\(t\)检验
根据之前求过的\(\mathbb{E}\{\boldsymbol{b}\}\)和\(\sigma^2\{\boldsymbol{b}\}\),加上
\[\frac{b_j-\beta_j}{s\{b_j\}}\sim t_{n-p}\]
由此可以检验\(H_0:\beta_j=0\),或求出\(\beta_j\)的置信区间(读者应当知道二者的联系)。 同样的,这也可以使用等效的\(F\)检验得到相同的结果。
预测值的置信区间与预测区间
同上,有
\[\frac{\widehat{\boldsymbol{Y}}_h-\widehat{\boldsymbol{X}}_h^\intercal\boldsymbol{\beta}}{s\{\widehat{\boldsymbol{Y}}_h\}}\sim t_{n-p}\]
求解预测区间时方差项只需多加一个\(\mathrm{MSE}\),即
\[\widehat{Y}_h\pm t_{1-\alpha/2,n-p}\sqrt{\mathrm{MSE}(1+\boldsymbol{X}_h^\intercal(\boldsymbol{X}^\intercal\boldsymbol{X})\boldsymbol{X}_h)}\]
系数的联合置信区间
Bonferroni Method是一个很常用,极其直观,而且效果也不会特别差的方式(除非维度特别高)。简单说,你如果需要构造\(X,\,Y\)的\(95%\)联合置信区间,你只需要分别构造\(X,\,Y\)的\(97.5%\)的置信区间然后合并(做笛卡儿积)即可。这是因为我们得到的联合置信区间,在\(X\)上没有覆盖真值的概率不超过\(2.5%\),记为事件\(A\);在\(Y\)上没有覆盖真值的概率不超过\(2.5%\),记为事件\(B\),则我们的联合置信区间没有覆盖真值的概率满足
\[\mathbb{P}(\overline{AB})=1-\mathbb{P}(AB)=1-\mathbb{P}(A)-\mathbb{P}(B)+\mathbb{P}(AB)\geq 1-\mathbb{P}(A)-\mathbb{P}(B)\geq 100\%-2.5\%-2.5\%=95\%\]
因此,如果你需要求取\(j\)个系数\(\beta_1,\ldots,\beta_j\)的联合置信区间(当然他们不需要相邻),只需要先计算Bonferroni系数\(B=t_{1-\alpha/(2j),n-p}\),然后使用各自的\(b_i,\,s\{b_i\}\)计算出各自的\(1-\alpha/j\)的置信区间,合并起来即为\(1-\alpha\)置信区间。
显然,这个信息没有充分利用起系数间的信息,而且考虑的是最坏的情况都能保证\(1-\alpha\)的置信水平。我们可以构造出更精细的置信区间,这在后面的方差分析会做进一步的阐述。
与残差相关的检验
Type-I SS and Type-III SS
\(\mathrm{SSR}\)表示该模型所带来的残差平方和的减少值。举例说
\[\mathrm{SSR}(X_2\lvert X_1)=\mathrm{SSE}(X_1)-\mathrm{SSE}(X_1,X_2)\]
可以很明显看到这里\(\mathrm{SSR}\)的值是两个模型的\(\mathrm{SSE}\)的差值,也就是\(X_2\)(在已引入\(X_1\))下的贡献。
而Type-I SS刻画的正是是依次加入变量后残差平方和较少的值,因此Type-I SS和模型中变量的顺序是有关的。
Type-III SS刻画的则是从全模型里抽取该变量后残差平方和的变化值。下面这个表可以更清楚的展现二者的关系
| Type-I SS | Type-III SS | |
|---|---|---|
| \(X_1\) | \(\mathrm{SSR}(X_1)\) | \(\mathrm{SSR}(X_1\lvert X_2,X_3)\) |
| \(X_2\) | \(\mathrm{SSR}(X_2\lvert X_1)\) | \(\mathrm{SSR}(X_2\lvert X_1,X_3)\) |
| \(X_3\) | \(\mathrm{SSR}(X_3\lvert X_1,X_2)\) | \(\mathrm{SSR}(X_3\lvert X_1,X_2)\) |
检验\(b_i=0\)
回忆之前给出过的更通用的形式,不难直接写出\(F\)检验的公式,这里面就用到了Type-III SS,并且知道这和上面的\(t\)检验是一致的。
\[F^\ast=\frac{\mathrm{SSR(X_j\lvert \cdot)/1}}{\mathrm{SSE}/(n-p)}\sim F_{1,n-p}\]
检验\(b_i=b_j=0\)
以三元回归为例,检验\(\beta_2=\beta_3=0\)。套用通用形式,直接写出
\[F^\ast=\frac{\mathrm{SSR(X_2,X_3\lvert X_1)/2}}{\mathrm{SSE}(X_1,X_2,X_3)/(n-4)}\sim F_{2,n-4}\]
而这里的\(SSR(X_2,X_3\lvert X_1)\)可以简单由\(SSR(X_2\lvert X_1)+SSR(X_3\lvert X_1,X_2)\)得到,也就是Type-I SS
更通用的检验形式
在使用SAS做分析时,其\(H_0\)的形式通常为\(\beta_j=\cdots=\beta_k=0\),因此对于其他的检验形式我们可能需要修改数据以套用现有的程序。
检验\(\beta_i=\beta_j\)
这类形式在协方差分析中的contrast一节有着更深入的讨论,这里只以最简单的\(\beta_1=\beta_2\)为例,模型为\(Y=\beta_0+\beta_1X_1+\beta_2X_2+\varepsilon\)
此时我们可以将模型写为 \[Y=\beta_0+\beta_1(X_1+X_2)+(\beta_2-\beta_1)X_2+\varepsilon\overset{\Delta}{=}\beta_0+\beta_1X_1^\ast+\beta_2^\ast X_2+\varepsilon\]
检验\(H_0:\beta_1=\beta_2\)即变为检验\(H_0:\beta_2^\ast=0\),因此对数据做简单变换后就可以使用先用的工具进行检验。
检验\(\beta_i=constant\)
很自然地,我们令\(Y^\ast=Y-constant\times\beta_i\)就能将\(H_0:\beta_i=constant\)变为\(H_0:\beta_i^\ast=0\)
决定系数与偏决定系数与偏相关系数
与一元回归一样,决定系数(coefficient of determination)定义为为\(R^2=\mathrm{SSR}/\mathrm{SSTO}\),衡量模型所能解释的方差比例。
而偏决定系数(coefficient of partial determination)则定义为\(r^2_{Y2\lvert 13}=\frac{\mathrm{SSR}(X_2\lvert X_1,X_3)}{\mathrm{SSE}(X_1,X_3)}\),衡量给定了\(X_1,X_3\)后,剩下的残差中能被这个“额外”的自变量所解释的比例。
与一元回归一样,\(r^2_{Y2\lvert 13}\)也可以由偏相关系数(coefficient of partial correlation)求得,即
\[r_{Y2\lvert 13}=corr(Y-\widehat{Y}(X_1,X_3),X_2-\widehat(X_2)(X_1,X_3))\]
可以看到偏相关系数是在现有的模型\(X_1,\,X_3\)下计算回归\(Y\)和额外自变量\(X_2\)的残差并求相关系数。
多重共线性问题
做多元回归分析中不可避免的一个问题就是多重共线性。简单说,由于自变量间存在的较强的相关性,使得我们对自变量的系数的估计不准(方差更大)。
一个浅显的例子就是,假设两个自变量\(X_1=X_2\)(即完全相关),而只用\(X_1\)拟合的结果可能是\(Y=0.1+0.3X_1\)。那么由于\(X_2\)的引入,你拟合的结果可能会是\(Y=0.1+0.1X_1+0.2X_2\),\(Y=0.1-100X_1+100.3X_2\)等。可以看到系数的方差极大,而且可能会干扰我们的判断(本来\(Y和X_1\)有一定正相关性,但在第二个模型中系数为\(-100\))。
当然,事实上由于数据的噪声,我们通常不会出现上面的退化情况,因此求出的最小二乘解仍然是唯一的。但你就无法得知你的最小二乘解落在了\(Y=0.1+0.1X_1+0.2X_2\)还是\(Y=0.1-100X_1+100.3X_2\)里,因为此时数据的小扰动就可能导致我们的系数发生剧变以“更好地拟合”数据。这也就是我们所说的“系数方差更大”。
多重共线性的诊断
不难发现,多重共线性的出现意味着你新引入的变量对于原始模型的方差没有解释力,并不能显著降低误差的大小,此时\(\mathrm{SSR}(X_{\mathrm{new}}\lvert R)\approx 0\)。因此如果我们发现了\(\mathrm{SSR}(X_1)\gg \mathrm{SSR}(X_1\lvert X_2)\),或\(r^2_{Y1}\gg r_{Y1\lvert 2}^2\)都揭示着共线性的存在。
VIF则是一个更常用的指标。其定义为
\[\mathrm{VIF}_j=\frac{1}{1-R_j^2}\]
其中\(R_j^2\)为使用其他变量回归\(X_j\)的决定系数\(R^2\)。不难发现\(\mathrm{VIF}_j\geq\frac{1}{1-r_{jk}^2},\forall k\neq j\),且对于二元情形有\(\mathrm{VIF}_1=\mathrm{VIF}_2=\frac{1}{1-r_{12}^2}\)
经验上,当最大的VIF>5的时候我们就需要更加谨慎的审查我们的模型,而当最大的VIF>10时,这样的模型几乎就是不可用的了,我们需要删除部分高度相关的因子来获得更加稳健的模型。
多重共线性的解决方案
All Subsets Regression
当自变量不太多的时候,我们可以跑所有的子集组成的模型,并根据某些准则选取最优的模型。
\(R^2\) criterion
显然我们不是去选择\(R^2\)最大的模型,要知道引入新的预测变量其\(R^2\)永远不会减少。所谓的\(R^2\) criterion其实是给出了一个阈值,我们在满足这个阈值的模型里选择最简单的。
\(R_a^2\) criterion
其实就是在\(R^2\)中引入对于模型复杂度,也就是自变量个数的惩罚,其定义为
\[R_a^2=1-\frac{n-1}{n-p}\frac{\mathrm{SSE}}{\mathrm{SSTO}}=1-\frac{\mathrm{MSE}}{\mathrm{SSTO}/(n-1)}\]
我们选择\(R_a^2\)最大的模型。
\(C_p\) criterion
\[C_p=\frac{\mathrm{SSE}}{\mathrm{MSE}(X_1,\ldots,X_{p-1})}-(n-2p)\]
选择\(C_p\)较小且接近\(p\)的模型。
AIC criterion
\[\mathrm{AIC}=n\log\mathrm{SSE}+2p\]
选择最小的AIC的模型。可以看到\(2p\)也是对模型复杂度的一个惩罚。事实上AIC也是一个应用相当广泛的指标,在贝叶斯模型选择中也有所涉及。
PRESS criterion
\[\mathrm{PRESS}=\sum_{i=1}^{n}(Y_i-\widehat{Y}_{i(i)})^2\]
其中\(\widehat{Y}_{i(i)}\)是只是用其他\(n-1\)个数据“拟合模型”然后预测出来的\(\widehat{Y_i}\),其实也就相当于留一的交叉验证。当然,我们不需要每次都重新拟合模型,而是有对应的公式直接计算\(\widehat(Y)_{i(i)}\)(见模型诊断的 Y-outlyers)。
Stepwise Regression
Forward Regression 从零开始,每次选择使得\(\mathrm{SSR}\)最大的变量并尝试加入(使用\(F\)检验),直到\(F\)检验不通过后流程中止。
Backward Regression 则从全模型开始,每次都选择Type-III SS最小的变量并尝试删除(使用\(F\)检验),直到\(F\)检验不通过后流程中止。
Lasso/Ridge Regression
由于多重共线性带来的是系数方差较大,一个可以采用的方式就是对其施加约束。Lasso/Regression是常用的方法,分别在优化目标里加上了\(L_1\)和\(L_2\)的惩罚项。一个形象化的解释如下图。Lasso的一个好处更容易使得切点出现在坐标轴上,起到了变量选择的作用。 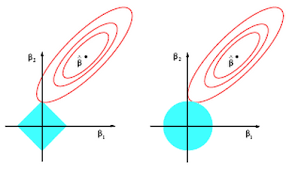
模型诊断
Partial Regressioni Plots
启发于片相关系数,对\(Y-\widehat{Y}(X_1,X_3)\)和\(X_2-\widehat{X_2}(X_1,X_3)\)进行做图,可以看到该变量的“净作用”,帮助用户检查该模型是否有潜在问题。
Y-outlyers
deleted residuals的定义为\(d_i=Y_i-\widehat{Y}_{i(i)}\),但我们不需要重新拟合模型,因为有如下关系
\[d_i=\frac{e_i}{1-h_{i,i}},\quad \sigma^2\{d_i\}=\frac{\sigma^2}{1-h_{i,i}}\]
其中\(h_{i,i}\)是\(\boldsymbol{H}=\boldsymbol{X(X^\intercal X)^{-1}X^\intercal}\)的第\(i\)个主对角线。
Studentized Deleted Residuals则定义为
\[t_i=d_i/s\{d_i\}=e_i/\sqrt{\mathrm{SSE}_{(i)}(1-h_{i,i})}\sim t_{n-p-1}\]
其中\(\mathrm{SSE}_{(i)}\) 为使用其他\(n-1\)个观测时的\(\mathrm{SSE}\)
实际计算时,同样无需重复拟合模型,因为有关系
\[t_i=e_i\sqrt{\frac{n-p-1}{\mathrm{SSE}(1-h_{i,i})-e_i^2}}\]
当然,你可以用这个值做\(t\)检验,但一般来说这个只会作为一个提醒你注意某些点的信息。
X-outlyers
检验\(X\)离群值只需考察\(h_{i,i}\)的值,也被称为 leverage value。
注意到有关系\(\sum_{i=1}^{n}h_{i,i}=p\),因此我们通常选取\(h_i>2p/n\),也就是两倍的均值来作为离群的指标。对这些点我们可能需要额外关注。
DFFITS, DFBETAS
这二者刻画着当减少一个数据点时,拟合结果和系数的波动。
\[\mathrm{DFFITS}_{(i)}=\frac{\widehat{Y}_i-\widehat{Y}_{i(i)}}{\sqrt{\mathrm{SSE}_{(i)}h_{i,i}}}\] \[\mathrm{DFBETAS}_{j(i)}=\frac{b_j-b_{j(i)}}{\sqrt{\mathrm{SSE}_{(i)}c_{j,j}}}\]
其中\(c_{j,j}\)是\(\boldsymbol{(X^\intercal X)^{-1}}\)的对角线(注意,\(\sigma^2\{\widehat{Y}\}=\sigma^2\boldsymbol{H},\,\sigma^2\{\boldsymbol{b}\}=\sigma^2\boldsymbol{(X^\intercal X)^{-1}}\))。
一个较常用的标准是,
\[\lvert\mathrm{DFFITS}_i\rvert>\left\{\begin{matrix} 2\sqrt{p/n} & n\quad \mathrm{large} \\quad 1 & \mathrm{o.w.}\end{matrix}\right.\]
\[\lvert\mathrm{DFBETAS}_{j(i)}\rvert>\left\{\begin{matrix} 2\sqrt{1/n} & n\quad \mathrm{large} \\quad 1 & \mathrm{o.w.}\end{matrix}\right.\]
Cook's Distance
Cook's Distance 则是 DFBETAS 的一个综合,其定义为
\[D_i=\frac{(\widehat\boldsymbol{Y}-\widehat\boldsymbol{Y}_{(i)})^\intercal(\widehat\boldsymbol{Y}-\widehat\boldsymbol{Y}_{(i)})}{p\mathrm{MSE}}=\frac{(\widehat\boldsymbol{b}-\widehat\boldsymbol{b}_{(i)})^\intercal(\boldsymbol{X^\intercal X})(\widehat\boldsymbol{b}-\widehat\boldsymbol{b}_{(i)})}{p\mathrm{MSE}}\]
一般的,我们关注超过0.8地,或者显著高于其他值的\(D_i\)。
- 本文链接:http://blog.vicayang.cc/Note-Multiple-Linear-Regression/
- 版权声明:本博客所有文章除特别声明外,均采用 CC BY-NC-ND 4.0 许可协议。转载请注明出处!