BMSI系列的第五篇,介绍贝叶斯计算中一个十分重要的算法——Metropolis Hastings
手敲\(\LaTeX\)难免出现纰漏,有任何疑似错误或者不清楚的地方请直接在下方评论区留言,谢谢各位读者。
M-H 算法
在高维空间中,上一节提到的简单采样方法往往不再奏效。此时我们使用另一个采样框架——MCMC。其核心思想是构造一个马尔可夫链Markov Cahin,其稳态分布为目标分布。然后通过在马尔可夫链上转移就完成了采样过程。本节提到的M-H算法 Metropolis-Hasting algorithm和下一节将提到的Gibbs sampling均属于这一框架。
下面我们记\(p(\theta\lvert y)\)为目标分布,\(\theta^{(t)}\)为\(t\)时刻我们采的样本。 M-H算法的框架如下
从提议函数(proposal)\(g(\theta\lvert\theta^{(t)})\)中获取一个提议\(\theta^\star\)(相当于前面的采样分布)
以概率\(\min\{1,r\}\)接受这个提议(\(\theta^{(t+1)}=\theta^\star\)),否则拒绝这个提议(\(\theta^{(t+1)}=\theta^{(t)}\))。其中
\[r=r(\theta^{(t)},\theta^\star)=\frac{p(\theta^\star\lvert y)/g(\theta^\star\lvert\theta^{(t)})}{p(\theta^{(t+1)}\lvert y)/g(\theta^{(t)}\lvert\theta^\star)}=\frac{p(\theta^\star\lvert y)}{p(\theta^{(t+1)}\lvert y)}\cdot\frac{g(\theta^{(t)}\lvert\theta^\star)}{g(\theta^\star\lvert\theta^{(t)})}\]
其证明我们放在下一节介绍。我们这里先考察两个特殊的提议函数——独立的提议函数(即满足\(g(\theta\lvert\theta^{(t)}=g(\theta)\))和对称的提议函数(即满足\(g(\theta\lvert\theta^{(t)}=g(\theta^{(t)}\lvert\theta\))
独立的提议函数
此时,\(r\)的表达式中第二项简化为\(g(\theta^{(t)})/g(\theta^\star)\)
例子
\(Y\sim\mathcal{N}(\theta,1)\),而参数有先验\(\theta\sim t_1(0,1)\),此时参数后验分布为
\[p(\theta\lvert y)\propto p(y\lvert\theta)p(\theta)\propto \frac{\exp\{-(y-\theta)^2/2\}}{1+\theta^2}\]
我们选择提议函数为\(\mathcal{N}(y,1)\),不难化简得此时
\[r=\frac{1+(\theta^{(t)})^2}{1+(\theta^\star)^2}\]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| MCMC <- function(n, burnout=0, start=0, seed=42) {
set.seed(seed)
N = n + burnout
samples = rep(NA, N)
current = start
for (i in 1:N) {
# set your proposal
proposal = rnorm(1, 1, 1) # y = 1
# set your ratio
logr = log(1 + current^2) - log(1 + proposal^2)
if (log(runif(1)) < logr) current = proposal
samples[i] = current
}
return(samples[(burnout+1):N])
}
N.factor <- integrate(function(x){exp(-(1-x)^2/2)/(1+x^2)}, -Inf, Inf)$value
posterior <- Vectorize(function(x){exp(-(1-x)^2/2)/(1+x^2) / N.factor})
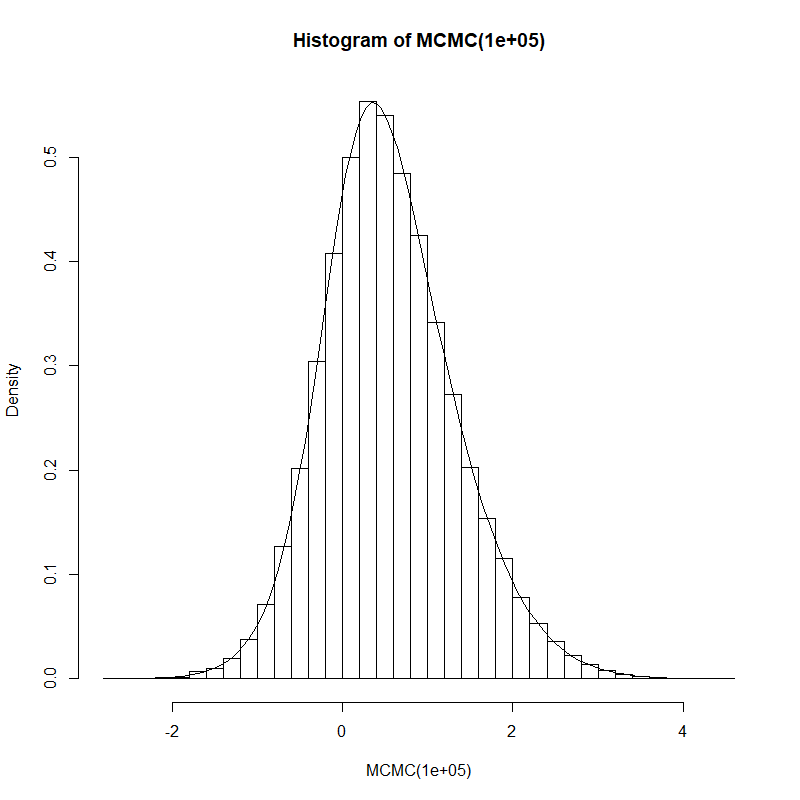
hist(MCMC(100000), prob=T, breaks=30)
curve(posterior, -2, 4, add=T)
par(mfrow=c(2,1))
plot(x=1:100, y=MCMC(100), pch=20, main="x_0=0")
plot(x=1:100, y=MCMC(100, start=1000), pch=20, main="x_0=1000")
|
重尾
回忆之前谈到的,拒绝采样法和重要性采样法都要求采样函数更加重尾,这里也不例外。否则,一旦\(\theta\)落入尾部,有\(p(\theta^{(t)}\lvert y)\gg g(\theta^{(t)})\),对于绝大多数提议\(\theta^\star\),有\(p(\theta^\star\lvert y)\approx g(\theta^\star)\),此时
\[r=\frac{g(\theta^{(t)})}{p(\theta^{(t)}\lvert y)}\frac{p(\theta^\star\lvert y)}{g(\theta^\star)}\approx 0\]
也就是说绝大多数采样都会被拒绝,我们的转移陷入了停滞。让我们举一个重尾的例子:后验分布为\(t_1\),而proposal使用\(\mathcal{N}(0,1)\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| MCMC <- function(n, burnout=0, start=0, seed=42) {
set.seed(seed)
N = n + burnout
samples = rep(NA, N)
current = start
for (i in 1:N) {
# set your proposal
proposal = rnorm(1)
# set your ratio
logr = dnorm(current, log=T) - dnorm(proposal, log=T) + dt(proposal, 1, log=T) - dt(current, 1, log=T)
if (log(runif(1)) < logr) current = proposal
samples[i] = current
}
return(samples[(burnout+1):N])
}
par(mfrow=c(3,1))
plot(x=1:1000, y=MCMC(1000), pch=20, main="x_0=0")
plot(x=1:1000, y=MCMC(1000, start=5), pch=20, main="x_0=5")
plot(x=1:1000, y=MCMC(1000, start=4, burnout=10000), pch=20, main="x_0=5, burnout=10000")
|
可以看到,一旦采样到\((-3,3)\)以外时,很容易就出现几十次的连续拒绝,这样的采样效果是很差的。而当初值极端时,甚至出现样本全部停滞的情况。一种对策是加入burnout的环节,使用一定的样本量进行“热身”,最后从“热身”后的起点开始抽样。但这也无法避免后续采样过程中出现极端样本后带来的影响,因此更明智的做法自然是仔细考察目标函数的性质,选用更加重尾的分布作为proposal。
对称的提议函数
此时,\(r=\frac{q(\theta^\star\lvert y)}{q(\theta^{(t)}\lvert y)}\),此时这通常也被称为随机游走的Metropolis算法。
根据\(r\)的形式,不难看出,这个算法的特性是,它会接受所有的“更好的提议”,而有一定概率接受“更差的提议”
例子
仍使用上面的例子,只是proposal不再使用\(\mathcal{N}(y,1)\)这一独立函数,而是使用\(\mathcal{N}(\theta^{(t)}, v^2)\)这一对称函数。在这里,我们先设置\(v^2=1\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| MCMC <- function(n, burnout=0, start=0, seed=42) {
set.seed(seed)
N = n + burnout
samples = rep(NA, N)
current = start
for (i in 1:N) {
# set your proposal
proposal = rnorm(1, current, 1)
# set your ratio
logr = -(1 - proposal)^2 / 2 + (1 - current)^2 / 2 + log(1 + current^2) - log(1 + proposal^2)
if (log(runif(1)) < logr) current = proposal
samples[i] = current
}
return(samples[(burnout+1):N])
}
N.factor <- integrate(function(x){exp(-(1-x)^2/2)/(1+x^2)}, -Inf, Inf)$value
posterior <- Vectorize(function(x){exp(-(1-x)^2/2)/(1+x^2) / N.factor})
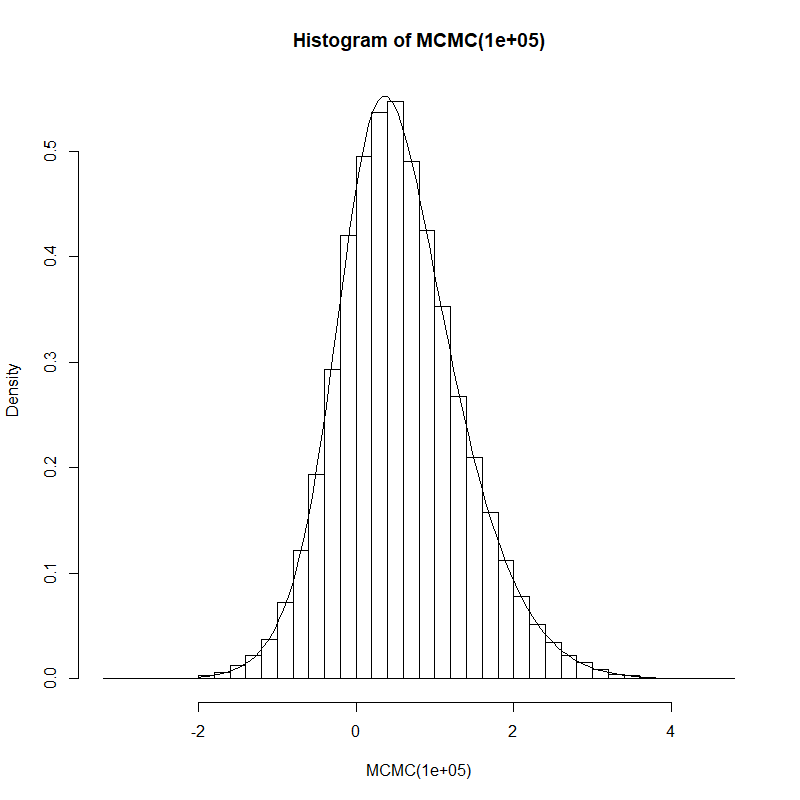
hist(MCMC(100000), prob=T, breaks=30)
curve(posterior, -2, 4, add=T)
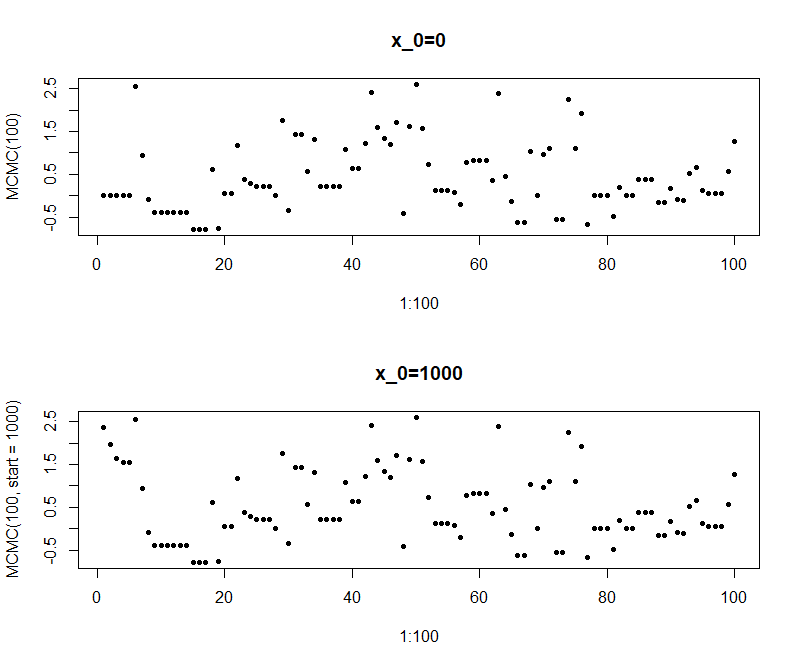
par(mfrow=c(2,1))
plot(x=1:100, y=MCMC(100), pch=20, main="x_0=0")
plot(x=1:100, y=MCMC(100, start=1000), pch=20, main="x_0=1000")
|
调参
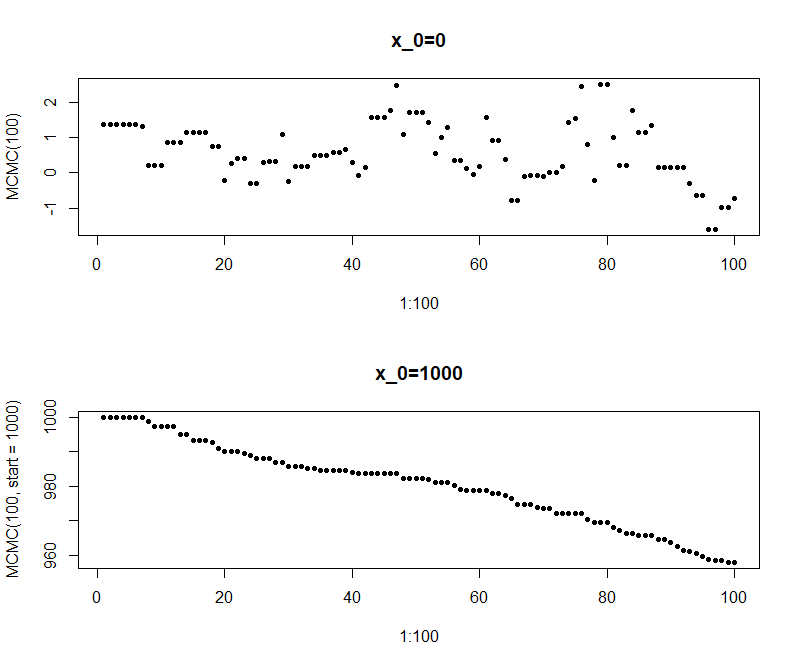
可以看到该方法也正确地完成了采样的工作。但当起始点偏离较多时,可以看到其采样的结果并非我们想要的——采样结果从1000缓慢的下降。可以想象,当我们设置一个较大的burnout后,采样工作可以步入正轨。但这仍是不让人满意的。为此,我们重新审视一下我们的采样过程。
我们每次的采样都是在前一步的基础上,在其周围选择下一个采样。而\(v^2\)控制的就是跳转的范围。当\(v^2\approx 0\)时,不难想象,每次的转移都只有极微小的变化,而此时的接受率\(r\approx 1\),因此我们总是接受这些样本——于是我们得到了一大堆集中在某一个小区域的样本,这显然不是一个好的采样。而且当起始值较差时,就会出现样本极其缓慢地往正确的区域移动的情形(即上面出现的)。
当\(v^2\)很大时又会怎样呢?显然此时\(\theta^\ast\)很容易就跑到很极端的值,也就意味着\(q(\theta^\ast\lvert y)\approx 0\),从而\(r\approx 0\)。此时绝大多数提议都被拒绝,采样效率也是极低的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| RW.MCMC <- function(n, sigma, burnout=0, start=0, seed=42) {
set.seed(seed)
N = n + burnout
samples = rep(NA, N)
current = start
for (i in 1:N) {
# set your proposal
proposal = rnorm(1, current, sigma)
# set your ratio
logr = -(1 - proposal)^2 / 2 + (1 - current)^2 / 2 + log(1 + current^2) - log(1 + proposal^2)
if (log(runif(1)) < logr) current = proposal
samples[i] = current
}
return(samples[(burnout+1):N])
}
par(mfrow=c(3,1))
plot(x=1:1000, y=RW.MCMC(1000, sigma=0.01), pch=20, main="sigma=0.01")
plot(x=1:1000, y=RW.MCMC(1000, sigma=1), pch=20, main="sigma=1")
plot(x=1:1000, y=RW.MCMC(1000, sigma=100), pch=20, main="sigma=100")
plot(x=1:1000, y=RW.MCMC(1000, start = 100, sigma=0.01), pch=20, main="sigma=0.01 start=100")
plot(x=1:1000, y=RW.MCMC(1000, start = 100, sigma=1), pch=20, main="sigma=1 start=100")
plot(x=1:1000, y=RW.MCMC(1000, start = 100, sigma=100), pch=20, main="sigma=100 start=100")
plot(x=1:1000, y=RW.MCMC(1000, start = 100, burnout=300, sigma=0.01), pch=20, main="sigma=0.01 start=100 burnout=300")
plot(x=1:1000, y=RW.MCMC(1000, start = 100, burnout=300, sigma=1), pch=20, main="sigma=0.01 start=100 burnout=300")
plot(x=1:1000, y=RW.MCMC(1000, start = 100, burnout=300, sigma=100), pch=20, main="sigma=0.01 start=100 burnout=300")
|
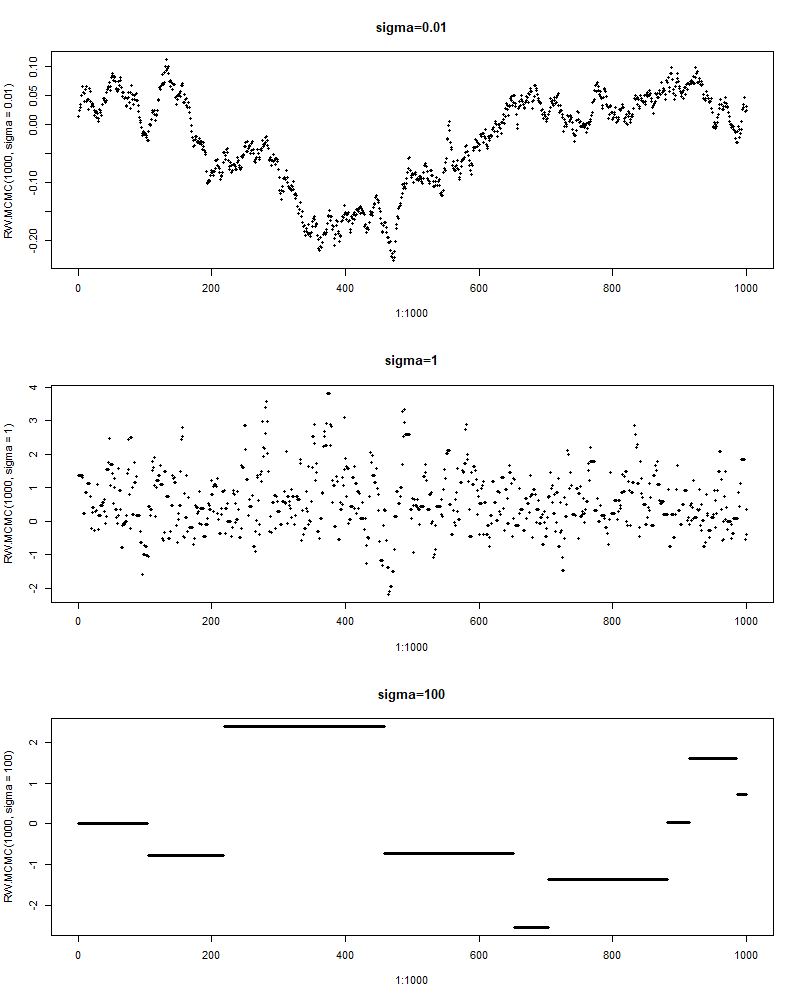
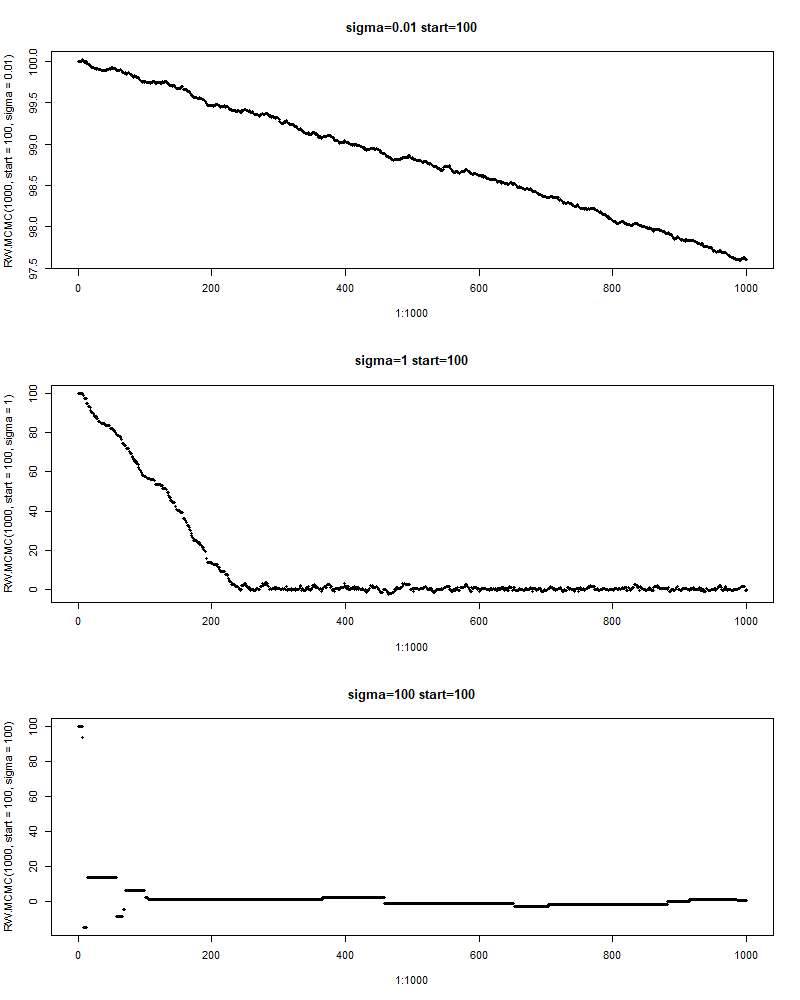
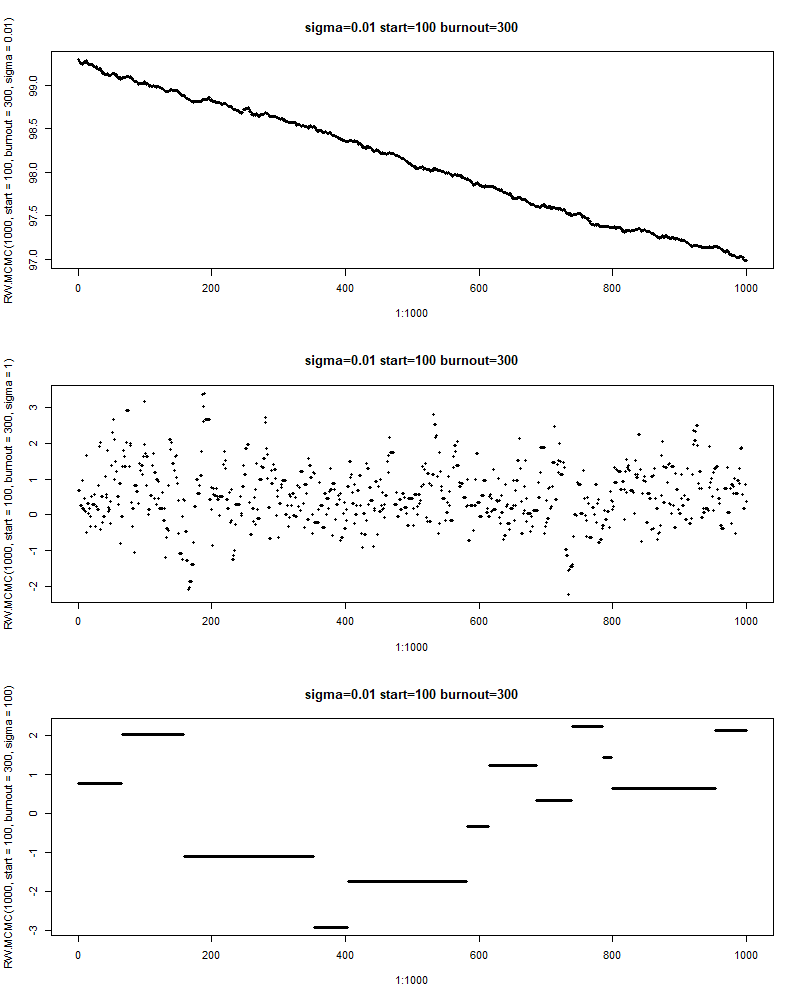
因此,应当存在一个合适的\(v^2\)来平衡大的跨度和高的接受率。然而手动尝试不同的\(v^2\)总不是一个好的解决方案。好在已有的一些研究表明,对于正态的proposal,最优的方差为\(2.4^2\mathrm{Var}(\theta\lvert y) / d\),其中\(d\)是参数\(\theta\)的维度。而这个最优的方差会使得接受率约为\(40\%\)(\(d=1\)),且随着参数维度的增加逐渐下降到\(20\%\)(\(d\rightarrow\infty\))。
那我们怎么获得\(\mathrm{Var}(\theta\lvert y)\)呢?能计算自然最好,如果难以计算,我们自然是使用抽样的方式来得到这个值的一个近似——只需要采出后验分布的样本然后计算方差即可。但这就牵扯到先有鸡还是先有蛋的问题了——我们求出这个值就是为了从后验分布采样而服务的,现在又要使用这个采样来求出这个值。因此,我们需要迭代式地进行这一过程。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| RW.Adapt.MCMC <- function(n, B, M, start=0, seed=42) {
set.seed(seed)
N = n + B * M
samples = rep(NA, N)
current = start
sigma = 1
for (b in 1:B) {
for (m in 1:M) {
i = (b - 1) * M + m
# set your proposal
proposal = rnorm(1, current, sigma)
# set your ratio
logr = -(1 - proposal)^2 / 2 + (1 - current)^2 / 2 + log(1 + current^2) - log(1 + proposal^2)
if (log(runif(1)) < logr) current = proposal
samples[i] = current
}
sigma = 2.4 * sd(samples[((b-1)*M):(b*M)])
}
for (i in (B*M+1):N) {
# set your proposal
proposal = rnorm(1, current, sigma)
# set your ratio
logr = -(1 - proposal)^2 / 2 + (1 - current)^2 / 2 + log(1 + current^2) - log(1 + proposal^2)
if (log(runif(1)) < logr) current = proposal
samples[i] = current
}
return(samples[(B*M+1):N])
}
N.factor <- integrate(function(x){exp(-(1-x)^2/2)/(1+x^2)}, -Inf, Inf)$value
posterior <- Vectorize(function(x){exp(-(1-x)^2/2)/(1+x^2) / N.factor})
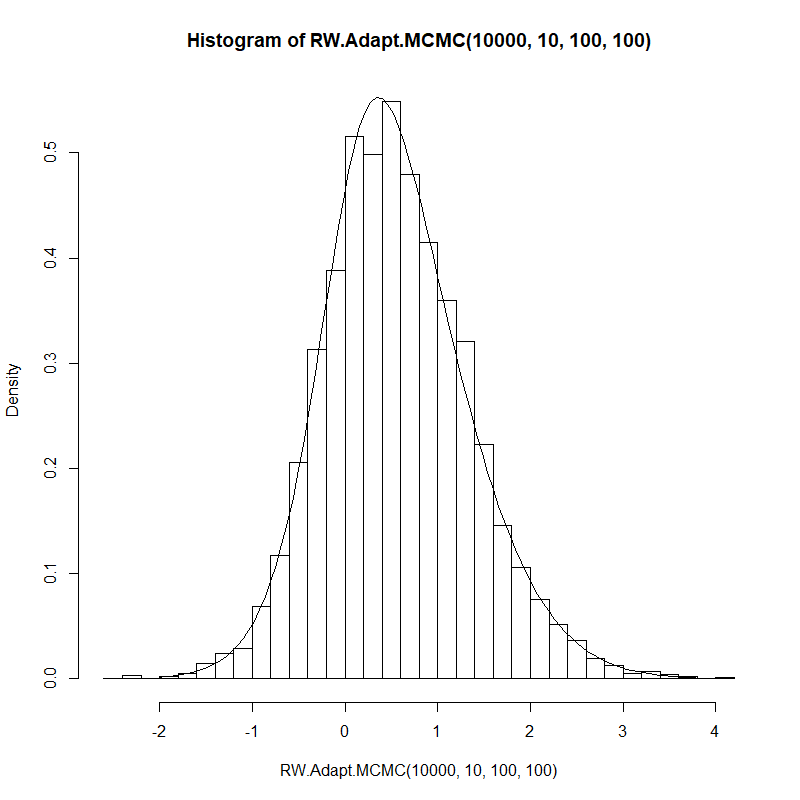
hist(RW.Adapt.MCMC(10000, 10, 100, 100), prob=T, breaks=30)
curve(posterior, -2, 4, add=T)
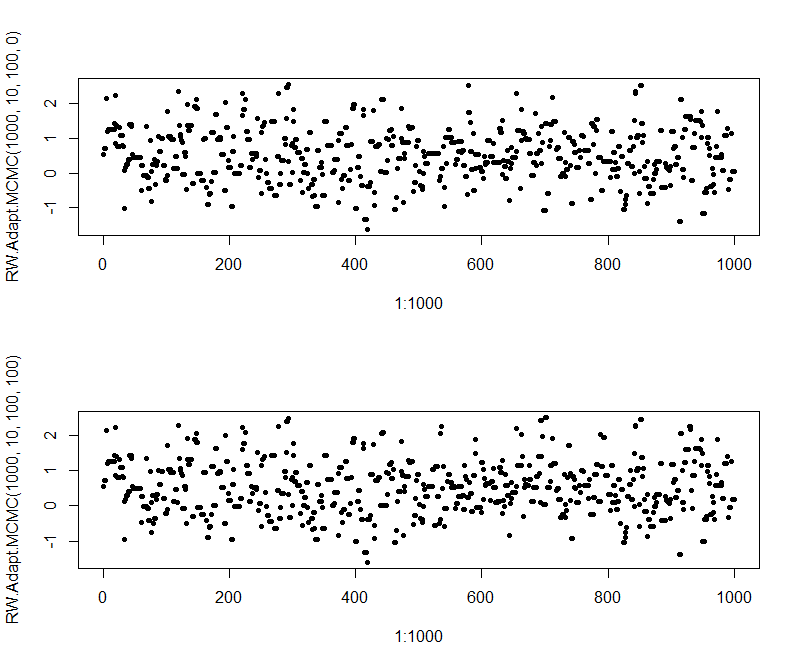
par(mfrow=c(2,1))
plot(x=1:1000, y=RW.Adapt.MCMC(1000, 10, 100, 0), pch=20)
plot(x=1:1000, y=RW.Adapt.MCMC(1000, 10, 100, 100), pch=20)
length(unique(RW.Adapt.MCMC(1000, 10, 100))) / 1000 # acceotance ratio 0.452
|