BMSI系列的第六篇，介绍贝叶斯计算中介绍用于多维分布中采样的Gibbs Sampling

手敲\(\LaTeX\)难免出现纰漏，有任何疑似错误或者不清楚的地方请直接在下方评论区留言，谢谢各位读者。

Gibbs Sampling

Gibbs Sampling的思想是，将高维空间的采样转化为若干个一维空间的采样，而这是我们所熟悉的。具体的，对于\(\theta=(\theta_1,\ldots,\theta_k)\)，我们的采样过程为

\[\begin{align} &\theta_1^{(t)}\sim p(\theta_1\lvert \theta_2^{(t-1)},\ldots,\theta_k^{(t-1)},y)\\ &\theta_2^{(t)}\sim p(\theta_2\lvert \theta_1^{(t)}, \theta_3^{(t-1)},\ldots,\theta_k^{(t-1)},y)\\ &\ldots\\ &\theta_i^{(t)}\sim p(\theta_i\lvert \theta_1^{(t)},\ldots,\theta_{i-1}^{(t)},\theta_{i+1}^{(t-1)},\ldots,\theta_k^{(t-1)},y)\\ &\ldots\\ &\theta_k^{(t)}\sim p(\theta_k\lvert \theta_1^{(t)},\ldots,\theta_{k-1}^{(t)},y)\\ \end{align}\]

当然，事实上每个\(\theta_i\)也并不要求是一个标量/长度为1的向量。如果你觉得\(\theta_i,\theta_{i+1}\)联合抽样更方便（比如是二元正态分布）也可以一次抽出。此时也叫做分块的Gibbs采样（block Gibbs sampling)

二元正态分布

我们首先用一个简单的例子来展示Gibbs Sampling。假设我们的目标分布为\(\theta=\left(\begin{matrix}\theta_1\\\theta_2\end{matrix}\right)\sim\mathcal{N}_2\left(\left(\begin{matrix}0\\0\end{matrix}\right),\left(\begin{matrix}1&\rho\\\rho&1\end{matrix}\right)\right)\)。根据概率论知识我们不难求得\(\theta_1\lvert\theta_2\sim\mathcal{N}(\rho\theta_2,1-\rho^2),\,\theta_2\lvert\theta_1\sim\mathcal{N}(\rho\theta_1,1-\rho^2)\)，于是乎

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Gibbs.example1 <- function(n, rho, start=c(0,0), seed=42) {
  set.seed(seed)
  sigma = sqrt(1 - rho^2)
  samples = matrix(NA, nrow=n, ncol=2)
  samples[1,] = start
  
  for (i in 2:n) {
    samples[i, 1] = rnorm(1, rho*samples[i-1, 2], sigma)
    samples[i, 2] = rnorm(1, rho*samples[i, 1], sigma)
  }
  return(samples)
}
samples = Gibbs.example1(1000, 0.8)
plot(x=samples[,1], y=samples[,2], pch=20)
colMeans(samples) 
# [1] -0.04617112 -0.04515437
cov(samples)
#           [,1]      [,2]
# [1,] 1.0121685 0.8152691
# [2,] 0.8152691 1.0126826

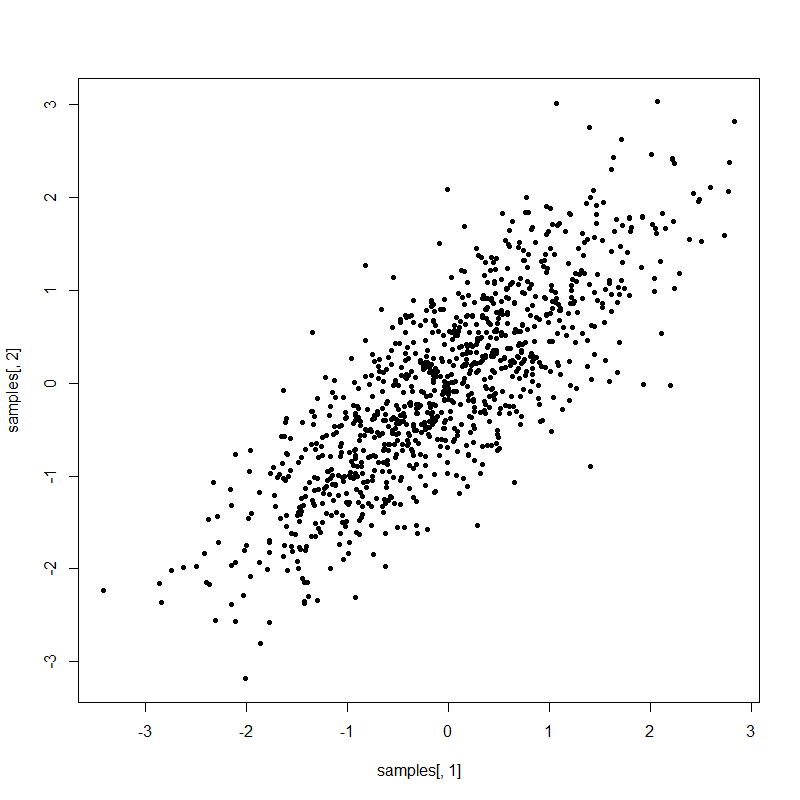
Gibbs + M-H

可以看到，Gibbs抽样的核心就是从\(p(\theta_i\lvert\theta_{-i},y)\)中进行抽样（\(\theta_{-i}\)表示除去\(\theta_i\)后的所有\(\theta\)）然而有时候从这个分布中直接抽样并不容易，于是我们可以嵌入M-H算法完成这一抽样。仍然使用上面的例子，但我们假装没办法完成\(\theta_2\lvert\theta_1\sim\mathcal{N}(\rho\theta_1,1-\rho^2)\)这一抽样，于是使用Randomwalk MH进行采样

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Gibbs.example1.2 <- function(n, rho, start=c(0,0), seed=42) {
  set.seed(seed)
  sigma = sqrt(1 - rho^2)
  samples = matrix(NA, nrow=n, ncol=2)
  samples[1,] = start
  
  for (i in 2:n) {
    samples[i, 1] = rnorm(1, rho*samples[i-1, 2], sigma)
    proposal = rnorm(1, samples[i-1, 2], 2.4*v) # Notice that 2.4*v is the optimal proposal sd
    logr = dnorm(proposal, rho*samples[i, 1], v, log=T)
         - dnorm(samples[i-1, 2], rho*samples[i, 1], v, log=T)
    samples[i, 2] = ifelse(log(runif(1))<logr, proposal, samples[i-1, 2])
  }
  return(samples)
}
samples = Gibbs.example1.2(1000, 0.8)
plot(x=samples[,1], y=samples[,2], pch=20)
colMeans(samples)
# [1] -0.04617112 -0.04515437
cov(samples)
#           [,1]      [,2]
# [1,] 1.0121685 0.8152691
# [2,] 0.8152691 1.0126826

参数扩张

参数扩张的思想是引入额外的参数，而目标分布则是扩张后的分布的一个边缘分布。我们通过在这个扩张后的空间内采样，也就得到了目标分布的采样。为方便计，我们假设目标的参数\(\theta\)是一个标量，目标分布为\(p(\theta\lvert y)\)。注意到

\[p(\theta\lvert y)=\int_0^{p(\theta\lvert y)}\,\mathrm{d}u\]

因此\(p(\theta\lvert y)\)可以视为下面这个均匀分布的一个边缘分布

\[(\Theta,U)\sim \mathrm{Unif}\{(\theta,u):\,0\leq u\leq p(\theta\lvert y)\}\]

因此我们的采样过程为

  1. \(u^{(t)}\lvert \theta^{(t-1)},y\sim \mathrm{Unif}\{u:\,0\leq u\leq p(\theta^{(y-1)}\lvert y)\}\)
  2. \(\theta^{(t)}\lvert u^{(t)},y\sim\mathrm{Unif}\{\theta:\,u^{(t)}\leq p(\theta\lvert y) \}\)

我们使用一个简单的例子，假设\(\theta\lvert y\sim \mathrm{Exp}(1)\)，即\(p(\theta\lvert y)=e^{-\theta}\)，此时\(\{\theta:\,u\leq p(\theta\lvert y) \}=(0,-\log(u))\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Gibbs.example2 <- function(n, start=1, seed=42) {
  set.seed(seed)
  u = rep(NA, n)
  samples = rep(NA, n)
  samples[1] = start
  
  for (i in 2:n) {
    u[i] = runif(1, 0, exp(-samples[i-1]))
    samples[i] = runif(1, 0, -log(u[i]))
  }
  return(samples)
}
hist(Gibbs.example2(10000), prob=T, breaks=30)
curve(exp(-x), 0, 8, add=T)

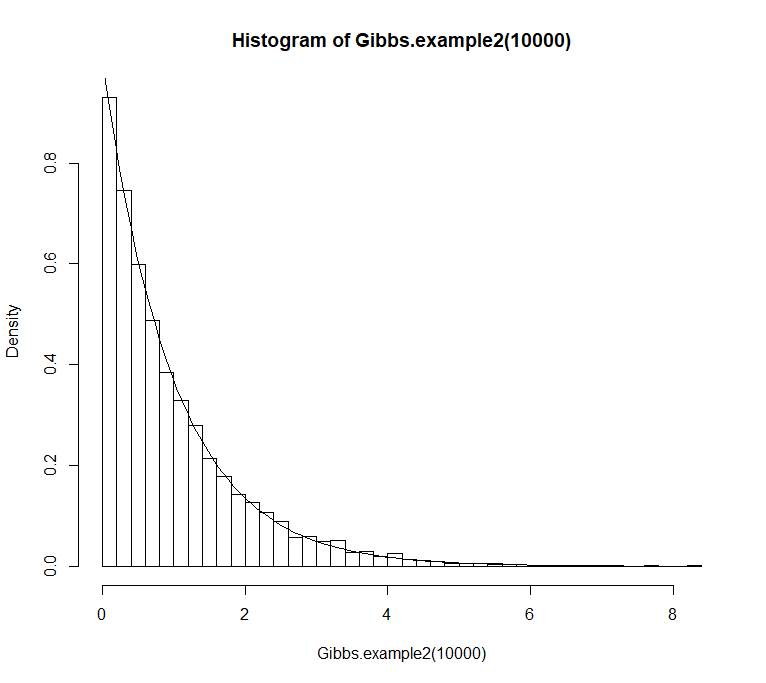
更多的例子

Hierarchical normal example

模型假设为\(Y_{ij}\sim\mathcal{N}(\mu_i,\sigma^2),\,\mu_i\sim\mathcal{N}(\eta,\tau^2)\)，其中\(i=1,\ldots,I.\,j=1,\ldots,n_i.\,n=\sum_{i=1}^{I}n_i\)。我们选取先验

\[p(\eta,\tau^2,\sigma^2)\propto\mathrm{Inverse-Gamma}(\tau^2,a_\tau,b_\tau)\cdot\mathrm{Inverse-Gamma}(\sigma^2,a_\sigma,b_\sigma)\]

可以推导出

\[\begin{align} p(\mu\lvert\eta,\sigma^2,\tau^2,y)&=\prod_{i=1}^{n}p(\mu_i\lvert\eta,\sigma^2,\tau^2,y_i)\\ p(\mu_i\lvert\eta,\sigma^2,\tau^2,y_i)&=\mathcal{N}(\mu_i;\left[\frac{1}{\sigma^2/n_i}+\frac{1}{\tau^2}\right]^{-1}\left[\frac{\bar{y}_i}{\sigma^2/n_i}+\frac{\eta}{\tau^2}\right]),\left[\frac{1}{\sigma^2/n_i}+\frac{1}{\tau^2}\right]^{-1})\\ p(\eta\lvert\mu,\sigma^2,\tau^2,y)&=\mathcal{N}(\eta;\bar{\mu}, \tau^2/I)\\ p(\sigma^2\lvert\mu,\eta,\tau^2,y)&=\mathrm{Inverse-Gamma}(\sigma^2;a_\sigma+n/2,b_\sigma+\sum_{i=1}^{I}\sum_{j=1}^{n_i}(y_{ij}-\mu_i)^2/2)\\ p(\tau^2\lvert\mu,\eta,\sigma^2,y)&=\mathrm{Inverse-Gamma}(\tau^2;a_\tau+I/2,b_\tau+\sum_{i=1}^{I}(\mu_i-\eta)^2/2) \end{align}\]

根据上式既可以完成Gibbs采样。

我们还可以选取另一个先验

\[p(\eta,\tau,\sigma)\propto\mathrm{Cauchy+}(\tau;0,b_\tau)\mathrm{Cauchy+}(\sigma;0,b_\sigma)\]

其中\(\mathrm{Cauchy+}\)为柯西分布只取正半轴的分布（乘二）。得到的形式与之前几乎一样，除了

\[\begin{align} p(\sigma\lvert\mu,\eta,\tau,y)&\propto\mathrm{Inverse-Gamma}(\sigma^2;a_\sigma+n/2,b_\sigma+\sum_{i=1}^{I}\sum_{j=1}^{n_i}(y_{ij}-\mu_i)^2/2)\mathrm{Cauchy+}(\sigma;0,b_\sigma)\\ p(\tau\lvert\mu,\eta,\sigma,y)&\propto\mathrm{Inverse-Gamma}(\tau^2;a_\tau+I/2,b_\tau+\sum_{i=1}^{I}(\mu_i-\eta)^2/2)\mathrm{Cauchy+}(\tau;0,b_\tau) \end{align}\]

此时从\(p(\tau\lvert\mu,\eta,\sigma,y)\)抽样就有许多方法了，比如

  • 使用独立的M-H算法，从\(\mathrm{Inverse-Gamma}\)中采样出\((\tau^\ast)^2\)，然后以接受率\(r=\mathrm{Cauchy+}(\tau^\ast;0,b_\tau)/\mathrm{Cauchy+}(\tau^{(t)};0,b_\tau)\)接受这一转移
  • 使用随机游走的M-H算法，使用某个对称的proposal\(g(\cdot\lvert\tau^{(t)})\)（如正态），然后以接受率\(r=p(\tau^\ast\lvert\mu,\eta,\sigma,y)/p(\tau^{(t)}\lvert\mu,\eta,\sigma,y)\)接受这一转移

Hierarchical binomial example

模型假设为\(Y_{ij}\sim\mathrm{Bin}(n_i,\theta-i),\,\theta_i\sim\mathrm{Beta}(\alpha,\beta)\)。我们选取先验\(p(\alpha,\beta)\propto(\alpha+\beta)^{-5/2}\)

可以推导出

\[\begin{align} p(\theta_i\lvert\cdots)&=\mathrm{Beta}(\theta_i;\alpha+y_i,\beta+n_i-y_i))\\ p(\alpha\lvert\cdots)&\propto(\prod_{i=1}^{n}\theta_i)^{\alpha-1}\cdot(\alpha+\beta)^{-5/2}/\mathrm{Beta}(\alpha,\beta)^n\\ p(\beta\lvert\cdots)&\propto(\prod_{i=1}^{n}(1-\theta_i))^{\beta-1}\cdot(\alpha+\beta)^{-5/2}/\mathrm{Beta}(\alpha,\beta)^n\\ \end{align}\]

注意这里的\(\theta_i​\)的抽样彼此是独立的，因此可以一起抽取，算是 block Gibbs sampling里一个特殊情形。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
log_alpha = function(theta, alpha, beta) {
  if (alpha < 0) return(-Inf)
  n = length(theta)
  return((alpha - 1) * sum(log(theta))
         - n * lbeta(alpha, beta) - 5 / 2 * (alpha + beta))
}
log_beta = function(theta, alpha, beta) {
  if (beta<0) return(-Inf)
  n = length(theta)
  return((beta - 1) * sum(log(1 - theta))
         - n * lbeta(alpha, beta) - 5 / 2 * (alpha + beta))
}
MCMC = function(n, dat, inits, tune) {
  n_groups = nrow(dat)
  alpha = inits$alpha
  beta = inits$beta

  samples = matrix(NA, nrow=n, ncol=2+n_groups)

  for (i in 1:n) {
    # Sample thetas
    theta = with(dat, rbeta(length(y), alpha+y, beta+n-y))
    # Sample alpha
    alpha_prop = rnorm(1, alpha, tune$alpha)
    logr = log_alpha(theta, alpha_prop, beta)-log_alpha(theta, alpha, beta)
    alpha = ifelse(log(runif(1))<logr, alpha_prop, alpha)
    # Sample beta
    beta_prop = rnorm(1, beta, tune$beta)
    logr = log_beta(theta, alpha, beta_prop)-log_beta(theta, alpha, beta)
    beta = ifelse(log(runif(1))<logr, beta_prop, beta)
    # Record parameter values
    samples[i,] = c(alpha, beta, theta)
  }
  colnames(samples) <- c('alpha', 'beta', paste('theta', 1:71, sep='_'))
  return(samples)
}

rats <- read.table("rats_data.txt",header=T)
inits = list(alpha=1, beta=1)
samples = MCMC(2000, dat=rats, inits=inits, tune=list(alpha=1,beta=1))

其中数据文件在层次化模型那一节出现过，为方便这里也放上链接数据。